Voici mon tout premier article (et j’espère que ce ne sera pas le dernier) sur le site de l’Esprit Sorcier ! J’attends donc vos avis avec impatience et je vous souhaites bonne lecture !

Ps : suite à un problème dans l’activation des commentaires pour cet article j’ai décidé de le copier, supprimer l’ancien et re-publier la copie en espérant que les commentaires soient activés pour cette copie… Enfin bref si vous le pouvez, n’hésitez pas a commenter ! 😉

Tout le monde le sait, les nombres servent à compter ! Ceci est vrai pour des nombres comme 1, 2, 3 etc… Mais pour un nombre tel que 0,6523 ? Ou même le nombre π ≈ 3,14159265359 ? Difficile de compter quelque chose à l’aide d’un nombre dont nous ne connaissons pas toutes les décimales…

Essayer de répondre aux deux questions ci-dessous constituera le fil rouge de cet article :

• Qu’est ce que compter ?
• Peut-on comparer la « taille » des ensembles de nombres ?

« Il y a trois sortes de personnes : celles qui savent compter et celles qui ne savent pas. »

1) Tout d’abord : qu’est ce qu’un ensemble de nombres ?

-Euh, eh bien c’est un ensemble dans lequel il y a des nombres non ?

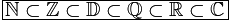
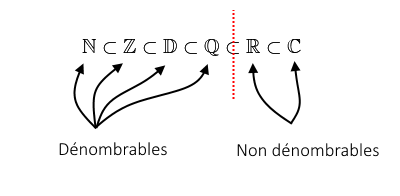
Voici différents ensembles de nombres, notés selon la tradition ancestrale avec leur « typographie à double barre ». Faisons les présentations :

• N l’ensemble des entiers naturels. Cet ensemble est constitué de nombres bien connus : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, et ceci jusqu’à l’infini. Ce sont les premiers nombres que l’on vient à manipuler lors de notre prime jeunesse et qui nous permettent de compter les objets. Ce détail sera en fait capital pour répondre à la question « Qu’est ce que compter ?« . Nous verrons au prochain paragraphe en quoi le fait de compter est lié à l’ensemble N.

-Ah oui, celui là je le connais !

• Z l’ensemble des entiers relatifs. Les entiers relatifs sont l’ensemble N des entiers naturels auquel nous avons ajouté les nombres négatifs :

…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …

-Hum… Oui, j’ai vu ça au collège il me semble…

• D l’ensemble des nombres décimaux. Voici trois exemples de nombres décimaux : 0,5 ; 5,475 ; 2354,000001. Les nombres décimaux peuvent posséder des décimales mais seulement en nombre fini. (Par exemple, π qui possède un nombre infini de décimales n’est pas un nombre décimal !)

• Q l’ensemble des nombres rationnels. Les nombres rationnels sont les nombres que l’on peut écrire comme un quotient de deux entiers relatifs c’est à dire les nombres de la forme a/b où a et b sont dans Z. Par exemple : 1/3 appartient à Q mais n’est pas dans D car 1/3 = 0,33333…, il possède une infinité de décimales. Il est intéressant de noter que durant l’Antiquité, les Grecs et notamment Pythagore considéraient qu’il n’existait pas d’autres nombres que les nombres rationnels positifs. Cette croyance fut, durant un certain temps, un frein dans l’évolution des mathématiques en occident puisqu’un résultat faisant intervenir des nombres non rationnels ou négatifs était alors considéré comme aberrant !

• R l’ensemble des nombres réels. Les nombres réels sont censés, comme leur nom l’indique, représenter tous les nombres que l’on peut rencontrer dans la réalité… Si nous représentons l’ensemble Z comme une succession de graduations sur une droite, alors les nombres réels constitueraient l’intégralité de la droite entre ces graduations :

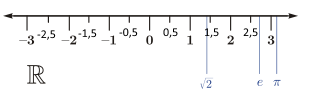
Nous remarquons, placés en bleu sur cette droite, des exemples de nombre réels qui ne sont pas dans l’ensemble Q, comme √2, π ou encore la constante de Neper e ≈ 2,71828182846. Ainsi, par exemple le nombre √2 ne peut pas s’écrire comme quotient de deux nombres dans Z.

-Donc cet ensemble contient tous les nombres existant ! Ah non ?

• C l’ensemble des nombres complexes. L’adjectif « complexe » ici ne signifie pas que ces nombres sont « plus compliqués » que les nombres réels, mais simplement que ces nombres sont formés d’un « complexe » de nombres réels. L’ensemble C doit contenir en particulier un nombre qui n’est pas réel. Appelons ce nombre « i » et posons : i = √(-1). Il se trouve que considérer la racine carrée d’un nombre négatif n’a pas de sens dans R, c’est pourquoi nous pouvons affirmer que le nombre i n’est pas un nombre réel. Ensuite pour obtenir le reste de l’ensemble des nombres complexes, il suffit de considérer tous les nombres de la forme :

z = a + ib

où a et b sont deux nombres réels quelconques. Notre nombre z a donc bien été écrit comme un « complexe » constitué de deux nombres réels. Il est intéressant de noter que si l’on représente l’ensemble R comme une droite, il est commode de représenter l’ensemble C comme un plan dont l’axe des abscisses est la droite réelle et l’axe des ordonnées la droite des « réels multipliés par le nombre i« . Ainsi, les coordonnées du nombre z dans ce plan sont le couple de nombres réels (a,b). Cette représentation permet de faire le lien entre géométrie du plan et nombres complexes. [1]

-Ah d’accord, donc en fait un nombre complexe c’est comme un couple de nombres réels !

Pour finir, il faut noter que le symbole « ⊂ » qui apparaît entre nos ensembles, dans la première image, signifie « est inclus dans« . Donc si l’on traduit en français ce qui est écrit dans la première image cela donne : « L’ensemble des entiers naturels est inclus dans l’ensemble des entiers relatifs qui est inclus dans l’ensembles des nombres décimaux etc. » Les ensembles que nous considérons sont donc « de plus en plus gros » au sens de l’inclusion. [2]

Maintenant que les présentations sont faites, nous allons pouvoir revenir à la question qui nous intéressait au départ : qu’est ce que compter ?

-Oui c’est vrai, on est là pour ça quand même !

2) Compter c’est mettre des objets en relation.

Comme nous l’avons laissé entendre dans le premier paragraphe, nous ne savons compter que grâce aux nombres entiers. Mais qu’est ce que compter ?

Si je vous demande « Combien y a-t-il de pommes sur cette image ? » vous allez, à coup sur, tendre le doigt devant vous et désigner les pommes l’une après l’autre tout en énumérant dans votre tête le début de l’ensemble N : « 1, 2, 3, 4, …« 

-Ah fastoche ! Je l’ai même fait sans tendre le doigt !

Ce-faisant vous allez en fait répondre à la question « qu’est ce que compter ? » ! Compter c’est associer à chaque pomme des nombres successifs de l’ensemble N. Comme ceci :

Et ? Et c’est tout… Oui cela paraît bête mais compter serait simplement associer à chaque objet un entier naturel dans l’ordre… Hum… Décevant…

-Et moi qui m’attendais à une révélation…

Mais trêve de plaisanteries, ne partez pas tout de suite !

C’est maintenant que les choses vont se gâter. Par exemple, si je vous donne le début de l’ensemble N jusqu’à 100 comme ceci :

0, 1, 2, …, 99, 100

Combien y a-t-il d’entiers ici ?

-Euh ben 100 ?

Si vous répondez 100, c’est faux !

-Et zut ! J’aurais dû me douter qu’il y avait un piège…

Evidemment il ne faut pas oublier de compter le nombre 0 ! Il y a donc 101 entiers ici. Cette erreur provient bien entendu du fait que l’on compte toujours en commençant par le nombre 1 et non 0. Comme nous l’avons fait pour les pommes, nous pouvons associer ici à chaque entier naturel de la liste ci-dessus, un entier naturel :

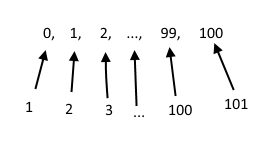
Le fait d’associer à chaque élément d’un ensemble A, un (et un seul) élément d’un autre ensemble B, s’appelle en mathématiques « construire une bijection entre les ensembles A et B ».[3]

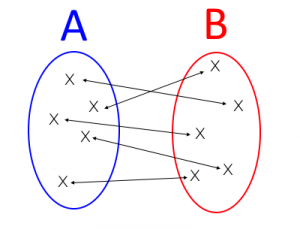
-Ahhh… Et donc dans l’exemple des pommes nous avons mis l’ensemble des 15 pommes en bijection avec l’ensemble des entiers naturels de 1 à 15 ? 😀

Exact ! Dans l’exemple où nous comptions les entiers naturels, nous avons construit une bijection entre l’ensemble des entiers naturels de 0 à 100 et l’ensemble des entiers naturels de 1 à 101 !

C’est en mettant en bijection l’ensemble N des entiers naturels et l’ensemble des entiers naturels privés de 0 (c’est à dire 1, 2, 3, 4, …) de la même façon que nous avons mis en bijection les entiers de 1 à 100 que l’on constate que compter les choses en commençant par 0 ou par 1 revient au même (quitte à décaler les indices d’une unité).

En mathématiques, il existe maintes façons de mettre deux ensembles en bijection et toutes ne sont pas aussi simples que nos deux exemples. La bijection est très commode pour montrer que deux ensembles (même si ils sont abstraits et que nous ne connaissons pas tous leurs éléments) « contiennent autant d’objets l’un que l’autre« .

Cela semble donc une bonne idée d’essayer de mettre les ensembles de nombres « en bijection » les uns avec les autres pour savoir si ils ont la même « taille » c’est à dire si ils contiennent le même nombre d’éléments.

3) Comparons les ensembles de nombres !

Cependant, il reste un problème que nous n’avons pas encore abordé… Les ensembles de nombres que nous souhaitons comparer sont… Infinis ! Ils contiennent donc tous une infinité d’éléments ! Ceci est d’ailleurs, très facile à vérifier : il est assez intuitif que l’ensemble N est infini, nous pouvons compter aussi loin que nous voulons, nous n’arriverons jamais au bout des nombres entiers !

-C’est vrai ça… Mais sait-on comparer des ensembles infinis ?

Il paraît assez intuitif que l’ensemble R des nombres réels contient « plus » de nombres que l’ensemble N… On le constate assez bien lorsque l’on représente les réels à l’aide de la droite réelle. Pourtant ils contiennent tous deux une infinité d’éléments et devraient donc être aussi « gros » l’un que l’autre !

C’est là qu’apparaît un autre avantage de la bijection : elle permet aussi de comparer des ensembles infinis !

-Trop fort la bijection !

Et pour nous y retrouver dans tout cela, nous devons introduire la notion d’ensemble dénombrable. Un ensemble A est dit dénombrable si nous pouvons le mettre en bijection avec N ou une partie de N.[4] C’est à dire qu’à chaque élément de A, nous allons pouvoir associer un entier naturel. Le mot « dénombrable » est bien adapté puisque nous allons pouvoir dénombrer -c’est à dire compter– les éléments d’un tel ensemble.

-Donc, comme on ne sait compter qu’en mettant les objets en bijection avec l’ensemble N, on saura compter les éléments des ensembles dénombrables  seulement ?

C’est bien cela ! Dans l’exemple des pommes, l’ensemble des pommes est  fini (il contient un nombre fini de pommes, 15 en fait), il est donc en particulier dénombrable, normal puisque nous avons associé à chaque pomme un nombre entier. Nous pouvons donc compter ses éléments. Mais il existe des ensembles dénombrables infinis !

Par exemple, l’ensemble N est le premier exemple d’ensemble dénombrable infini. Nous pouvons mettre l’ensemble N en bijection avec lui même de façon triviale (à chaque entier naturel nous lui associons lui même !). Nous savons donc compter les éléments de l’ensemble N.

-Ok, donc maintenant on sait compter les nombres qui nous permettent de compter ! Quoi ?!

COMPARONS LES ENSEMBLES N ET Z.

L’ensemble Z des entiers relatifs peut être mis en bijection avec N : il est donc dénombrable. Cependant il faut rester prudent et ne pas s’y prendre n’importe comment ! En effet, essayons d’associer à chaque élément de Z un élément de N de manière « naïve » :

-Mais ? Mais ? On n’y arrivera jamais !

Cette méthode simpliste est vouée à l’échec ! En effet, une fois que nous aurons épuisé notre stock d’entiers naturels dans N en les associant aux entiers relatifs positifs, il ne nous en restera plus pour compter les entiers relatifs négatifs !

-C’est donc peine perdue ? On ne peut pas dénombrer l’ensemble Z ?

Pas tout à fait ! Il suffit en réalité de changer légèrement notre stratégie. Il faut que nous gardions autant d’entiers naturels pour compter les entiers positifs que les entiers négatifs… Nous allons donc alterner numérotation d’un nombre positif et numérotation d’un nombre négatif comme ceci :

Nous comptons les éléments de Z, en associant à 0 le nombre 0 puis en associant 1 à 1, 2 à -1 et nous continuons en alternant nombre positif et nombre négatif ! Ainsi, nous allons bien réussir à associer un entier naturel à chaque entier relatif ! On constate ainsi que l’ensemble N et l’ensemble Z sont en bijection.

-Ouf ! Mais c’est quand même étrange…

On peut noter au passage que si on regarde uniquement les nombres positifs sur la droite dans l’image ci-dessus, nous avons également mis en bijection les entiers naturels (qui sont les entiers relatifs positifs) avec les entiers naturels impairs !

En un sens il y a donc autant d’éléments dans N que dans Z !

-Mais on dirait pourtant que Z contient deux fois plus de nombres de N…

Surprenant non ? Cependant attention ! Ce n’est pas pour autant que les ensembles N et Z sont égaux ! On voit clairement que l’ensemble Z contient l’ensemble N mais contient en plus des nombres qui ne sont pas dans N (comme -1 par exemple) !

-Donc si je comprend bien, N et Z ont le même nombre d’éléments mais l’un est plus gros que l’autre ??

Cela vient du fait que la notion de « nombre d’éléments » n’a plus de sens lorsque l’on considère des ensembles infinis ! C’est pourquoi, en toute rigueur, il est préférable de dire que deux ensembles infinis sont en bijection plutôt qu’ils « contiennent le même nombre d’éléments ».

-Ah ok ! 😀 Bon finalement ce n’était pas si difficile que ça ! Au suivant !

COMPARONS LES ENSEMBLES N ET R.

Attaquons nous maintenant à l’ensemble R des nombres réels, qui lui, semble vraiment plus « gros » que l’ensemble Z.

-Cette fois-ci, j’en suis sur, il y a plus de nombres réels que de nombres entiers naturels !… C’est vrai hein ?

En effet, il ne sera pas possible de dénombrer R et nous pouvons le prouver ! Pour cela nous allons montrer que l’intervalle [0;1] n’est pas dénombrable ! (Nous appelons intervalle [0;1] l’ensemble des nombres réels compris entre 0 et 1 inclus.) 

-Donc si [0;1] n’est pas dénombrable, comme R contient [0;1], R ne sera pas dénombrable non plus !

Nous devons montrer que nous ne pouvons pas compter les éléments de [0;1] ! Et pour faire cela il nous faut compter des éléments de [0;1] en utilisant entièrement l’ensemble N puis, trouver un élément de [0;1] que nous n’avons pas compté…

Ainsi, imaginons avoir trouvé un ensemble dénombrable dans [0;1]. C’est à dire que nous avons réussi à compter certains éléments de [0;1] à l’aide de N. Notons :

r₁, r₂, r₃, r₄, r₅, r₆, …

ces éléments. Chaque élément r_i (pour i étant un entier naturel) est un nombre réel dans l’ensemble [0;1], il s’écrit donc sous la forme « 0,… » (ou éventuellement 0 ou 1) avec éventuellement une infinité de décimales à droite de la virgule.

L’idée maintenant va être de construire un élément de [0;1] différent de tous les r_i.

-Facile ! Il suffit de choisir un élément de [0;1] au hasard ! Avec un peu de chance nous tomberons sur un nombre différent des r_i !

Mais il y a un souci avec cette méthode !

-Arf, il y a toujours un hic…

En effet, espérer tomber au hasard sur un élément de [0;1] différent des r_i, c’est supposer qu’un tel élément existe. Or c’est précisément ce que nous voulons montrer. Nous devons donc construire « à la main » un tel élément.

Prenons un exemple simple. Supposons que nos r_i soient au nombre de 5 :

r₁=0,24621 ;  r₂=0,22458  ;  r₃=0,93147

r₄=0,01475  ;  r₅=0,10451

Nous allons construire le nombre S appartenant à [0;1], différent de tous les r_i, comme ceci :

On regarde successivement la i^ième décimale de r_i (c’est à dire la 1^ère décimale de r₁, puis la 2^ème décimale de r₂, etc.) :

Si cette décimale n’est pas un 1 alors la i^ième décimale de S sera un 1.

Si cette décimale est un 1 alors la i^ième décimale de S sera un 2.

De sorte que dans tous les cas, la i^ième décimale de S soit différente de la i^ième décimale de r_i .

Appliquons cette méthode à nos 5 éléments de [0;1] :

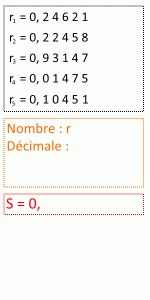
Le nombre S que nous venons de construire est donc :

S=0,11212

Il appartient bien à l’intervalle [0;1] et est bien différent de tous nos r_i.

-Ouais mais il y a une arnaque là ! A partir de la deuxième décimale de S, on savait déjà qu’il était différent de tous les r_i !

Certes, mais cela vient du fait que nous avons pris un exemple particulier. En effet, il faut également pouvoir appliquer cette méthode peu importe les r_i que nous avons choisis dans [0;1] ! Donc comme cette preuve doit fonctionner pour n’importe quels r_i, nous ne pouvons pas dire que le nombre S est différent des tous les r_i à partir du moment où l’on a choisi (par exemple) sa seconde décimale. En effet, nous pourrions toujours trouver un exemple pour lequel r_i posséderait les deux même premières décimales que S et ainsi la preuve ne fonctionnerait plus dans ce cas particulier…

-Mais alors, pourquoi ça marche ?

Ça marche car nous construisons S de façon à ce que ça marche ! En effet, le nombre S est construit de sorte que sa i^ième décimale soit toujours différente de la i^ième décimale de r_i et donc que S soit différent de r_i et ce pour tous les r_i.

-Ah ! Et donc même si un des r_i possède les mêmes premières décimales que S, leurs i^ièmes décimales seront de toute façon toujours différentes et donc S sera différent de r_i !

Exact !

-Mais… Attends un peu, et si l’un des r_i n’a pas de i^ième décimale ? Par exemple, si je choisi r_i=0 ?

Eh bien ce n’est pas vraiment un problème, il suffit alors de considérer que 0 s’écrit aussi : 0,000000000… avec une infinité de « 0 » derrière la virgule. Ainsi la i^ième décimale de 0 sera… 0 !

-Ah ouf !

Il ne reste maintenant plus qu’à reproduire cette expérience avec autant de r_i qu’il y a d’éléments dans N et le tour est joué : nous aurons construit un élément de [0;1] différent de tous les r_i, c’est à dire que nous n’avons pas compté ! Donc [0;1] n’est pas dénombrable ! [5]

-Yes ! L’ensemble des réels non dénombrable : check !

Comme l’ensemble [0;1] des réels compris entre 0 et 1 n’est pas dénombrable, l’ensemble R tout entier ne l’est pas non plus !

4) Et que dire des ensembles D, Q et C ?

Il existe des démonstrations similaires à celle que nous avons tenue pour montrer que l’ensemble Z est dénombrable, prouvant que les ensembles D et Q sont également dénombrables. Il est enfin assez clair que l’ensemble C ne peut pas être dénombrable, en effet C contient l’ensemble R qui lui même n’est pas dénombrable !

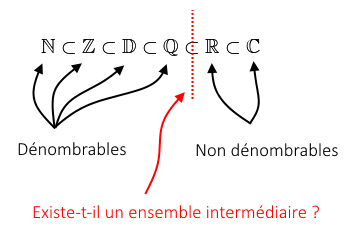
Nous pouvons constater dans un premier temps qu’il y a une rupture dans la propriété d’être dénombrable au delà de l’ensemble Q :

Et dans un second temps, tous les ensembles dénombrables sont de taille comparable à celle de l’ensemble N (au sens de la bijection). Cependant, il est possible de démontrer que tous les ensembles non dénombrables ne sont pas en bijection avec R, il existe des ensembles plus « gros » que R au sens de la bijection ! Il est en effet possible de construire un exemple d’ensemble non dénombrable qui n’est pas en bijection avec l’ensemble des réels.

En bref :

Nous savons « compter » au sens de la dénombrabilité (c’est à dire de la bijection) tous les éléments des ensembles inclus dans l’ensemble Q des nombres rationnels : ils sont tous aussi « gros » que l’ensemble N.

Nous ne pouvons pas toujours mettre en bijection deux ensembles non dénombrables.

5) Des ensembles infinis dénombrables « dans la vraie vie » ?

Il est tout à fait possible de rencontrer des ensembles dénombrables dans le vrai monde de la réalité véritable ! La preuve :

-Haha super marrant vraiment…

Plus sérieusement, il n’est pas si compliqué de rencontrer un ensemble dénombrable dans la vraie vie. Par exemple, l’ensemble (que nous appelerons A) des mots que l’on peut écrire à l’aide d’un alphabet contenant un nombre fini de lettres est un ensemble dénombrable. Evidemment, cet ensemble A ne contient pas que les mots qui ont un sens, sinon il serait fini (et donc trivialement dénombrable). Si cet ensemble était infini les dictionnaires prendraient alors des proportions assez problématiques… Imaginons que A est l’ensemble des mots que l’on peut écrire à l’aide de l’alphabet français (c’est à dire l’alphabet latin moderne). Dans cet ensemble nous trouverions alors des mots comme : « a », « b », « c », « aa », « abbaaacc », « ztdvvjhea », etc. Le terme « mot » signifierait donc ici plus une succession de lettres, qu’un vrai mot. Ainsi, cet ensemble est infini et dénombrable.

-Et t’as une preuve de ça ?

Oui ! Il existe des preuves. Mais voici un argument assez intuitif : notre ensemble A est très similaire à l’ensemble N des entiers naturels. Nous pouvons voir l’ensemble N comme l’ensemble des mots que l’on écrit à l’aide de l’alphabet : {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Ainsi, comme N est infini dénombrable, l’ensemble A l’est également. Evidemment, l’alphabet de l’ensemble A peut contenir plus de « lettres » que l’alphabet de N. Mais ce n’est pas un problème tant que cet alphabet contient un nombre fini de lettres.

-Ah ok ! Donc l’ensemble A c’est un peu comme N.

6) Un peu d’histoire des Maths.

Le mathématicien Russe Georg Cantor (1845-1918) [6] est notamment célèbre pour avoir bousculé les certitudes des mathématiciens du début du XXème siècle, en démontrant que l’ensemble R des nombres réels est non dénombrable, grâce à l’argument diagonal (dit « argument diagonal de Cantor ») qui est la preuve que nous avons vu plus haut. Cette démonstration tient son nom du fait que nous avons parcouru les décimales des r_i « en diagonale ». Il est en fait à l’origine de la définition d’ensemble dénombrable/non dénombrable. Il publia également des preuves de la dénombrabilité d’ensembles comme NxN, Q ou encore l’ensemble des nombres algébriques.[7] Il est l’un des premiers à travailler avec la notion d’infini en la considérant comme un objet plutôt que de la considérer comme quelque chose d’impossible à appréhender. Il va également émettre une conjecture appelée « Hypothèse du continu » qui pose la question suivante :

Existe-t-il un ensemble de taille intermédiaire entre celle des ensembles dénombrables et celle des ensembles non dénombrables ? [8]

Autrement dit : existe-t-il un ensemble non dénombrable (qui n’est pas en bijection avec N ou une partie de N) que nous ne pouvons pas mettre en bijection avec R ?

Ou encore : existe-t-il un ensemble qui n’est ni en bijection avec N (ou un partie de N), ni en bijection avec R ?

Cette hypothèse qui est restée célèbre jusqu’à aujourd’hui est encore un sujet de recherche pour certains mathématiciens. Elle a été partiellement résolue par le mathématicien Austro-Américain Kurt Gödel (1906-1978) [9] à l’aide du  Théorème d’incomplétude portant son nom.[10] Gödel affirme à l’aide de ce théorème que l’hypothèse du continu fait partie des résultats indécidables de la théorie des ensembles ZFC [11] (pour faire simple : la théorie « classique » des mathématiques).

-Ça veut donc dire qu’un tel ensemble n’existe pas dans cette théorie ?

Ce résultat signifie juste que la théorie classique des mathématiques ne suffit pas pour pouvoir décider de l’existence ou non d’un tel ensemble ! Autrement dit, dans cette théorie nous ne pouvons ni prouver qu’un tel ensemble existe ni prouver qu’il n’existe pas !

Conclusion.

Si compter paraît être un acte naturel et intuitif à première vue, ce n’est pas pour autant que la question du dénombrement est vide d’intérêt. Comme nous l’avons vu, elle a nécessité notamment l’introduction de la bijection, qui est une notion puissante et centrale des mathématiques contemporaines. Si elle a bouleversé la pensée mathématique du XXème siècle, elle a su cependant entraîner Cantor et ses successeurs dans une réflexion profonde sur la notion d’infini et la notion d’ensembles de nombres dans le but de comprendre et de formaliser rigoureusement ces objets mathématiques.

Pensez-y la prochaine fois que vous mangerez une pomme ! 😉

• [1] Le plan complexe : Plus d’informations sur le plan complexe ici !
• [2] Un petit schéma pour mieux comprendre l’inclusion des ensembles de nombres !
• [3] Voici une définition rigoureuse d’une bijection : soient A et B deux ensembles, une bijection est une application f : A → B vérifiant : tout élément y de l’ensemble B admet un et un seul antécédent x dans A tel que f(x)=y.
• [4] Une partie de N est un sous-ensemble de N, par exemple l’ensemble {0, 1, 2} est une partie de N, l’ensemble des nombres entiers naturels pairs en est une autre.
• [5] Un lien concernant l’argument diagonal.
• [6] Plus d’informations sur notre ami Cantor ici !
• [7] Pour les plus courageux, des compléments sur les ensembles dénombrables et non dénombrables !
• [8] Un document un peu perché sur la théorie des ordinaux de Cantor et l’hypothèse du continu !
• [9] Plus d’informations sur notre ami Gödel !
• [10] Pour ceux qui n’ont pas froid aux yeux, plus d’informations sur le théorème d’incomplétude de Gödel ! (Bonne chance)
• [11] Petit complément aussi accessible que possible sur la théorie ZFC.

En espérant que cet article beaucoup plus long que prévu vous ait plu !

A bientôt ! 😉