Bonjour, je vais vous parler de la téléportation quantique. Sous ce nom racoleur qui rappelle la science fiction se cache un protocole de communication qui utilise la mystérieuse mécanique quantique.

Pourquoi je parle de la téléportation quantique ?

J’avais envie de parler de ce protocole car on entend beaucoup parler de lui, et il circule beaucoup de choses à son sujet, qui parfois… sont un peu fausses, voir même sans aucun sens: Alors parfois on entend parler de transfert d’information instantané mais qui respecterait la relativité restreinte… ce qui est antithétique au possible. D’autres fois on lit ça (cf wikipedia):

On constate alors que l’état du qubit d’Alice est téléporté sur le qubit de Bob dans 25 % des cas lorsque Alice mesure pour ces deux qubits les états binaires 0. Dans les autres cas, Alice doit transmettre à Bob le résultat de ces mesures, appelées mesures de Bell, afin que ce dernier puisse finaliser la téléportation.

ce qui est inexacte et révèle une certaine incompréhension de la chose.

En même temps le protocole repose sur un des plus incompréhensible, des plus difficiles à saisir, des moins bien compris phénomènes de la mécanique quantique, la si fameuse intrication quantique.

C’est donc pour éclaircir les choses que je vais essayer d’expliquer ce que c’est que cette satané téléportation.

Mais alors c’est quoi cette téléportation quantique ?

Première chose à comprendre, c’est qu’on téléporte un état quantique, et pas une particule, ni aucune autre matière. Seul de l’information passe d’un endroit à un autre. C’est pourquoi je vais introduire la téléportation avec un équivalent classique (non quantique quoi…)

Une analogie classique du protocole de téléportation.

On peut dans une certaine mesure, avoir un équivalent classique du protocole. On va avoir affaire ici à nos deux protagonistes préférés Alice et Bob. On va dire que nos deux amis vont manipuler des petits boîtiers dotés d’un écran et d’un gros bouton au milieu. Quand ils appuient sur le bouton, un nombre va apparaître à l’écran, ce sera soit un 0 soit un 1. Ce nombre est enregistré dans le boîtier mais il est impossible de dire, avant d’appuyer sur le bouton, ce qui va s’afficher à l’écran.

Le but du jeu va ếtre pour Alice d’envoyer à Bob la valeur d’un boîtier qu’on appellera « a » sans qu’Alice ne puisse appuyer sur le bouton de « a ».

Mais pourquoi elle pourrait pas appuyer ? ce serait plus simple…

Bah parce que ce sont les règles du jeu ! Na. Pour être plus précis cette règle est là pour calquer une règle de la mécanique quantique, mais j’y reviendrai dans la partie quantique du protocole.

Cependant, Alice pourra agir sur les boîtiers avec certaines opérations, telles qu’addition, multiplication etc… (mais modulo 2… j’en parlerai plus loin).

Bon accouche ! Ils font comment alors ?

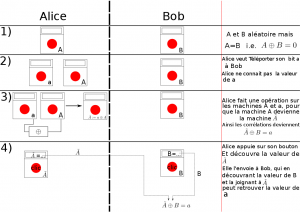
Alors:

• Première étape ils vont avoir chacun un boîtier bien particuliers: « A » pour Alice et « B » pour Bob. Ils sont particuliers, car même si on ne connaît pas leur valeur, on sait que A=B. C’est à dire si quand Alice appuie sur le bouton de « A » et qu’un 1  s’affiche, alors quand Bob appuiera ce sera aussi un 1. Si c’est 0, c’est 0 pour les deux. On dit que les valeurs des boîtiers sont corrélées.
• Deuxième & troisième étapes, Alice possède deux boitiers, « a » et « A », et Bob possède « B ». Alice va brancher « a » et « A » affin de faire la somme modulo 2…

  Hop hop hop !! C’est quoi ce truc de modulo là… t’as dit que tu nous expliquerais

  Alors c’est tout simple, on ne peu additionner que des 0 ou 1, et donc on a 0+0=0 mod2, 1+0=0+1=1 mod2 et 1+1=0 mod2.
  … Je disais donc, Alice fait la somme modulo 2 (c’est à dire qui suit la règle précédante) des valeurs de « A » et « a », pour la mettre dans la machine « A », on va donc l’appeler « A’ « , ainsi on peut dire que A’=A+a mod2.

• Quatrièmement, Alice appuie sur le bouton de « A’  » (mais pas de « a » hein !! ) voit le résultat et l’envoie à Bob. De son côté Bob appuie sur son bouton, obtient la valeur de « B ». Quand il reçoit la valeur de « A’ « , il l’ajoute modulo 2 à sa valeur de B ce qui lui donne la valeur de « a ». Et voilà !!

Attends un peu, pourquoi quand Bob ajoute A’ et B ça fait a ?

Alors on a dit que A’=A+a mod2, donc A’+B=A+B+a mod2. Or on sait que A=B, donc A’+B=B+B+a mod2. Et B+B=0 mod2 (vérifiez avec la règle que j’ai donnée). D’où A’+B=B+B+a=0+a=a mod2 CQFD.

Important: Je tiens à préciser, que dans l’étape 3, l’information sur la valeur de « a » n’est pas dans A’ , ni dans B, elle est dans leur corrélation. Si ici cela semble assez naturelle, c’est moins évident dans la version quantique !

Le Vrai Protocole de téléportation quantique

Dans la version quantique du protocole, on va téléporter un état, et pour rester simple on se limite aux états de systèmes à deux niveaux…

Oulalala ! De quoi tu nous parles là ?

Un peu de mécanique quantique préliminaire

J’y arrive ne vous en faites pas. Un système à deux niveaux est un système quantique qui, quand on le mesure ne donne que deux valeurs possibles. Par exemple on peut prendre le spin d’un électron, ou d’une autre particule de spin 1/2, ou bien encore la polarisation d’un photon, ou une boite quantique à deux niveaux d’énergie ou alors …

ça va on a compris ! Tu nous embrouilles là…

Bref, ces systèmes à deux niveaux on les appelle qubits (pour qu[antum] bits). On va donc téléporter un qubit, alors que dans l’analogue classique on a téléporté un bit.

Bon, le truc c’est qu’un qubit c’est un peu plus compliqué qu’un bit. Un bit ne prend que deux valeurs possibles: 0 ou 1. Un qubit peut prendre une infinité de « valeurs », mais pour une mesure donnée, on en mesurera toujours que deux !

Ça y est, dès que c’est quantique on y comprend plus rien…

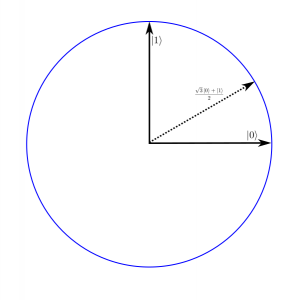
Mais non, je vous explique. En fait un état quantique (pas forcément à deux niveau d’ailleurs) n’est pas représenté par un nombre comme pour les bits, mais par un vecteur (de longueur 1)! Vous savez les trucs qui ressemblent à des flèches, en cours de maths de collège ou de lycée ! Bah là c’est exactement (presque) les mêmes ! Donc pour tous ceux qui se posaient la question, oui les vecteurs ça sert ! 🙂 Mais ne vous en faites pas on va pas trop faire de maths ici, c’est pas le but.

Donc je disais, un état est représenté par un vecteur de longueur 1. On en prendra deux qui vont former un angle droit, il y en aura un qu’on appellera |0> et l’autre |1> (regardez sur la Figure 2). On appelle ces deux vecteurs, les vecteurs de base, et l’ensemble des états possibles forme un cercle: à chaque point du cercle correspond un état.

Maintenant quand on mesure: si l’état est sur |0> alors après la mesure il va rester |0>, et on va mesurer 0. Pareil pour |1>, après la mesure rien ne change et on mesure 1. Mais pour tous les autres vecteurs, ils vont être projetés aléatoirement sur |0> ou sur |1>, et on va mesurer soit 0 soit 1 selon que  le vecteur est projeté sur |0> ou sur |1>. Quand je dis aléatoirement, en fait la projection pendant la mesure va se faire avec une certaine probabilité qui dépend de l’angle que fait le vecteur avec les vecteurs de base (du produit scalaire pour être plus précis): Par exemple dans la figure 2, le vecteur représenté qui ne fait pas partie de la base, a plus de chance de se projeter sur |0> que sur |1> car l’angle qu’il forme avec |0> est plus petit que celui qu’il forme avec |1>.

Vous vous rappelez dans le protocole classique la règle qui disait qu’Alice ne peut pas appuyer sur le gros bouton ? Et bien c’est à cause du fait qu’ici en mécanique quantique quand on mesure, on change l’état, et du coup on sait pas dans quel état était le qubit avant la mesure, donc pas moyen de dire à Bob quel était cet état. Il faut donc faire autrement. Et dans le protocole classique c’est justement pour faire autrement que de regarder la valeur de « a » et l’envoyer à Bob que j’ai interdit à Alice de regarder (enfin c’est parce que c’est quantique quoi…).

Bon maintenant je vais pouvoir attaquer le protocole à proporement parler

Le protocole de téléportation quantique

Bon, bah c’est simple, suffit de faire comme en classique ! Voilà, vous savez tout !

Eh !!! Mais on veut des explications nous !! Sinon on irait voir les Bogdanov !!

Ca va ça va, je vais expliquer. Alors on va procéder en 4 étapes comme dans le cas classique.

• Première étape, Alice est Bob se partagent un état intriqué (un des 4 états de Bell). Dans la figure 3 on peut voir l’expression de cet état.

  Eh beh ! toi qui disais qu’on n’allait pas faire de maths…

  En effet, on n’en fera pas. On va juste voir ce que veulent dire ces expressions. Alors pour commencer, les constantes comme 1/2 ou racinne(2) on peut les oublier, elles sont juste là pour que les vecteurs aient une longueur de 1. Sinon on peut voir dans ces expressions qu’on ajoute des termes à deux ou trois qubits. Cela veut dire que l’état est un « mélange » de chacun des termes de la somme, et que quand on va mesurer, l’état va se projeter sur un de ces termes. Par exemple, dans la première étape, Alice et Bob se partagent un état où il y a une somme de deux termes de chacun deux qubits; un truc du genre |0>|0>+|1>|1>. Donc ça veut dire que quand il vont mesurer, l’état va se projeter sur |0>|0> OU sur |1>|1>, et donc ils vont toujours mesurer soit 1 tout les deux soit 0 tout les deux, mais jamais 0 pour Alice est 1 pour Bob car le vecteur ne se projette jamais sur |0>|1>. Et c’est bien parce qu’Alice et Bob mesurent toujours les mêmes valeurs qu’on dit que leur état est intriqué.
  Pour ceux qui veulent en savoir un peu plus, un état intriqué se dit aussi état non séparable, car on ne peut pas écrire l’état en question comme le produit d’un état d’un qubit de Bob par celui d’un qubit d’Alice. Un exemple d’objet « non séparable » serait le polynôme xy+x²y². On ne peut pas l’écrire sous forme d’un polynôme qui ne dépend que x multiplier par un polynôme qui ne dépend que de y, c’est-à-dire, on ne peut pas séparer les x et les y. Pour les états non séparables c’est pareil, on ne peut pas séparer ce qui est à Alice de ce qui est à Bob.

• Deuxième étape, Alice prend le qubit qu’elle veut le téléporter (l’état |Φ>), et le fait interagir avec le qubit qui est intriqué avec celui de Bob. D’un point de vue des expressions, on multiplie juste l’état intriqué à deux qubits, par l’état du qubit |Φ>. Ca forme donc un état à trois qubits. Ce qui est intéressant c’est que cet état peut s’écrire sous une autre forme où l’état |Φ> se trouve du côté de Bob (regardez dans la figure 3, le |Φ> a un indice B). On approche du but. Cela dit le prix à payer c’est qu’un opérateur U (une transformation si on veut)  se trouve devant notre |Φ>. Cet opérateur vient modifier |Φ>, va falloir régler ce problème. Et en plus pour chaque terme l’opérateur U change (on voit qu’il y a un k en indice), il y a donc 4 opérateurs qui modifient |Φ>.  Heureusement Bob sait tout de même quels sont ces quatres opérateurs (se sont les opérateurs représentés par les matrices de Pauli). Mais pour l’instant Bob ne peut pas faire grand chose.
• Dans la troisuème étape, Alice va faire une mesure appelée mesure de Bell. Cette mesure est particulière car elle mesure deux qubits en même temps, en le projetant sur un des 4 états de Bell (qui sont 4 états maximalement intriqués, c-à-d avec des corrélations parfaites). Alice va alors mesurer une valeur N (où N est 1,2,3 ou 4), qui correspond au terme de la somme sur lequel l’état de l’étape deux va se projeter. L’état s’étant projeté sur un des 4 termes la somme, disparaît. De plus on voit que cet état est le produit d’un état de deux qubits d’Alice par un qubit de Bob; c’est un état qui est séparable ! On va donc pouvoir traîter séparément ce qui se passe du côté d’Alice de ce qui se passe du côté de Bob. Mais il reste toujours le problème du U qui est toujours là. Comme il y a 4 U possibles, Bob ne sait pas quelle opération il faut faire pour enlever ce U. Il faut que Bob sache quel U se trouve devant |Φ> pour qu’il puisse faire la transformation qui enlève U (tranformation qu’on appelle transformation inverse de U, ou opérateur inverse de U).
• Alice va donc envoyer la valeur N qu’elle a obtenue à Bob. Ainsi Bob saura quel est le U qui se trouve devant |Φ> et pourra donc appliqué la bonne transformation, et donc avoir |Φ> ! Et voilà le qubit est téléporté

Quelques remarques maintenant.

– On peut d’abord noter que chaque étape de la téléportation trouve son équivalent classique.
– Puis il est important de comprendre qu’à l’étape 3, Bob n’a pas d’information sur |Φ>, et ce à cause de indétermination sur le U. En fait le fait qu’il y ait 4 possibilités et qu’il ne sache pas laquelle est la bonne lui cache toute l’information. Par ailleurs Alice n’a plus l’information non plus. C’est dans la corrélation entre la valeur N que possède Alice et le U correspondant du côté de Bob que se trouve l’information. Et donc pour avoir l’information il faut que les deux bouts soient au même endroit, c’est pourquoi Alice envoie N à Bob. Et cet envoi elle le fait de manière classique. C’est à dire par téléphone, fax, email etc. Et donc la valeur de N va voyager à la vitesse de lumière (au maximum), il n’y donc pas de transfert instantané d’information, c’est pourquoi la téléportaton quantique respecte la relativité.

Voilà Je crois que j’ai fini, et j’espère que les explications sont claires… Si vous avez des questions ou remarques laissez un commentaire.