Un problème bien embarrassant
Résoudre des équations du 3e degré grâce à Jérome Cardan
Un mathématicien italien du XVIe siècle appelé Jérome Cardan a formulé une formule pouvant résoudre les équations du type :
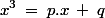
Ici, x, p et q sont chacun des nombres réels, on dit qu’ils appartiennent à l’ensemble des réels et on le note ainsi :

Cependant ce type d’équation n’était résolvable en cette époque qu’à certaines conditions; il faut en effet que :

Lorsque la condition précédente est respectée, alors les solutions sont :

On peut également écrire de cette manière (c’est équivalent) :

Bombelli, le petit futé qui travaille avec l’impossible !

En 1572, le mathématicien italien Bombelli décide d’utiliser la formule de Cardan en s’autorisant à utiliser des nombres considérés comme impossible comme sqrt(-121), sans essayer à en comprendre se sens.
PS : sqrt = « square root » en anglais, qui se traduit par « racine carrée » en français.
Nous allons maintenant vérifier que sqrt(-121) est bien solution de l’équation :

A l’aide de la formule de Cardan, on obtient :






On aboutit donc à :




Une histoire de notation
Un problème avec la notation sqrt(-1)
En 1774, le mathématicien allemand Carl Friedrich Gauss estime que la notation sqrt(-1) pose un problème car en effet :

Or pour sqrt(-1), on abouti à une contradition car :

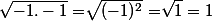
D’un côté on obtient 1 et (-1), il y a donc un problème avec cette notation.
Une nouvelle notation apparait
En 1777, le mathématicien suisse Leonhard Euler décide de noter sqrt(-1) de cette manière :
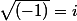
Euler propose que sqrt(-1) est égal à i (comme imaginaire); en l’élevant au carré, on obtient :
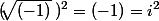
Au final, on se retrouve avec des nouveaux nombres appelés <<imaginaires>> qui respectent :

Vers l’ensemble des nombres complexes
Un nouvel ensemble de nombre encore plus grand que les réels est alors apparu. On décide de noter cet ensemble C (pour nombres complexes).
Un nombre complexe se note souvent z et vérifie les conditions :
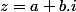
Ici, a et b sont des nombres réels et i est le nombre tel que :

Votre ensemble de nombre ressemble maintenant à cela :

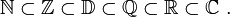

Pour un peu plus détailler la composition de chaque ensemble, on a :
Cette illustration nous montre bien que l’ensemble des complexes C est l’association de l’ensemble des réels R avec l’ensemble des nombres imaginaires I.






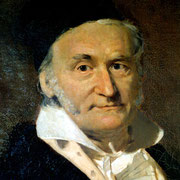





Franchement, merci beaucoup ! C’est très bien expliqué, et en plus, simple à comprendre. Je n’ai pas un très grand niveau, mais j’ai compris ce que je voulais comprendre. Alors merci !
Je suis fières d’eux.
merci beaucoup c’est bien expliqué
il y a une erreur après Bombelli le petit futé . ce sont des 4 au lieu des 8 sous les racines cubique .
merci beaucoup c’est très bien expliqué
Excellente démonstration
Merci du fond du cœur
Très bonne illustration, c’est correct
Excellent démonstration