Bonjour à tous! Comme promis à certains d’entre vous, ce mois-ci sera consacré à la mathématicienne Sophie Germain.

BIOGRAPHIE:

Née à Paris le 1^er avril 1776, Marie-Sophie Germain était une mathématicienne et philosophe française, descendante d’une ancienne famille d’orfèvres de la bourgeoisie parisienne. A l’âge de 13 ans, elle commence à s’intéresser aux mathématiques suite à la lecture d’un chapitre sur la mort d’Archimède, tué d’un coup d’épée par un soldat alors qu’il traçait des cercles sur le sol pendant la prise de Syracuse par les Romains. Elle apprend seule la théorie des nombres, branche des mathématiques qui s’occupe des propriétés des nombres entiers (qu’ils soient réels ou relatifs) ainsi que le calcul différentiel et intégral, et ce en étudiant les travaux d’Euler et de Newton.

Les sciences étant une « affaire d’hommes », son père tente de la dissuader de s’orienter vers une profession « masculine » et lui confisque les chandelles qu’elle utilise pour étudier la nuit. Devant sa détermination, il accepte finalement de la soutenir sur le plan moral et financier. Elle suit alors les cours de l’Ecole Polytechnique par correspondance sous le nom d’un ancien élève, Antoine-Auguste Le Blanc, car les femmes n’étaient pas admises dans cette prestigieuse école jusqu’en 1972.

Elle devient l’amie de Joseph-Louis Lagrange, professeur d’analyse à l’Ecole Polytechnique, et de Carl-Friedrich Gauss avec qui elle correspond sous le même nom d’Antoine-Auguste Le Blanc avant de lui révéler son identité après que, craignant pour la sécurité de son ami pendant la guerre franco-prussienne, elle demande au général Pernety de veiller sur lui.

Gauss la recommande pour un poste honorifique à l’université de Göttingen mais elle meurt d’un cancer du sein le 27 juin 1831 à Paris, avant l’attribution de cette distinction.

Elle apporte des contributions importantes à l’étude de l’élasticité, théorie des petites déformations continues et réversibles des milieux dont les propriétés élastiques sont les mêmes dans toutes les directions. Elle effectue également des études sur la théorie des nombres avec comme découverte la plus notable, la démonstration partielle du théorème de Fermat.

THÉORÈME DE FERMAT ET DÉMONSTRATION PARTIELLE :

Le théorème de Fermat est au départ fondé sur le théorème de Pythagore, selon lequel, dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.

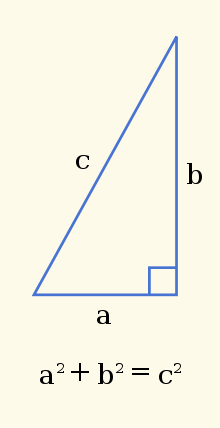
Illustration du théorème de Pythagore

    Le dernier théorème de Fermat représente une généralisation de ce dernier : l’équation xⁿ+yⁿ=zⁿ n’admet aucune solution pour n>2 (la condition n=2 correspondant au théorème de Pythagore). Celui-ci sert notamment au cryptage à clef publique-clef privée (cryptage RSA).

Sophie Germain démontre ce théorème pour certains cas particuliers. C’est le théorème de Sophie Germain :

1^er cas :

Si n>2 est premier, ainsi que 2n+1

Alors xⁿ+yⁿ=zⁿ implique que l’un des nombres x, y ou z est divisible par n.

2^ème cas :

Si p impair et 2p+1 sont premiers

x^p+y^p=z^p n’admet aucune solution si le produit xyz n’est pas divisible par p.

NB : p est ici un nombre premier dit « de Sophie Germain », ce qui signifie que c’est un nombre premier tel que 2p+1 soit lui aussi un nombre premier. 2p+1 est appelé « nombre premier sûr ».

    Elle rédige également, lors de ses recherches, trois mémoires pour expliquer théoriquement le phénomène de vibration des lames élastiques trouvé expérimentalement par le physicien Ernst Chladni, dont celui publié en 1816, intitulé Mémoires sur les vibrations des lames élastiques. Ce dernier lui valut le prix des sciences mathématiques à l’Académie des Sciences la même année.